Giường trộn đồng nhất (Phần 1)
Trong một kho chứa đồng nhất nguyên liệu thô, một đống được rải bởi số lớn lớp, sau đó chúng được rút ra theo cách nào đó sao cho tất cả các lớp đã rải đều có mặt trong vật liệu được rút ra. Để tính hiệu quả trộn trên lý thuyết có thể mong đợi từ những điều kiện như vậy, ta cần nhắc một chút về lý thuyết thống kê. Chúng tôi xin giới thiệu bài dịch của kỹ sư Lê Văn Tiệp.
>> Giường trộn đồng nhất (Phần 2)
Giới thiệu:
Trên nguyên tắc, mọi người chấp nhận rằng số lớp trong một giường trộn là yếu tố quyết định đối với độ đồng nhất thu được. Theo cái gọi là lý thuyết thống kê của giường trộn, sự giảm độ sai lệch tiêu chuẩn từ các nguyên liệu đầu vào đến các nguyên liệu đầu ra có quan hệ với căn bậc hai của số lớp nguyên liệu được rút đồng thời. Tuy nhiên, với các kho chứa có liên quan đến khái niệm trung bình động (điển hình là kho tròn vận hành theo phương thức Chevron liên tục), thời gian các loạt thay đổi thành phần của nguyên liệu đầu vào đóng vai trò phụ và đáng kể. Đây là phân tích trên lý thuyết bằng thống kê đại cương và có dính líu tới cỡ hạt liên quan đến khối lượng mẫu trong đánh giá các phép thử trộn.
Trong một kho chứa đồng nhất nguyên liệu thô, một đống được rải bởi số lớn lớp, sau đó chúng được rút ra theo cách nào đó sao cho tất cả các lớp đã rải đều có mặt trong vật liệu được rút ra. Để tính hiệu quả trộn trên lý thuyết có thể mong đợi từ những điều kiện như vậy, ta cần nhắc một chút về lý thuyết thống kê.
Bối cảnh thống kê.
Đặc tính của các thông số ngẫu nhiên là không bao giờ biết chính xác được giá trị của nó. Số phép đo có thể thực hiện và từ các phép đo này đánh giá sự phân bố hay tính toán định lượng các tính chất (như giá trị trung bình, hiệp biến, …). Để xác định cách định lương các tính chất này ra sao, hãy xem xét thông số ngẫu nhiên X và giả sử rằng một số phép đo cụ thể độ lớn của thông số này đã được thực hiện. Đã quan sát được các giá trị sau x1, x2, …, xn và chúng xuất hiện với tần suất f(x1), f(x2), … , f(xn), ở đây:
Giá trị mong đợi E[X] (tức là giá trị mong muốn nhất) của thông số ngẫu nhiên của chúng ta X được xác định là giá trị trung bình:
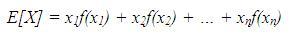
Các giá trị mong đợi của toán tử E[] sẽ luôn luôn liên quan đến trọng lượng, một thông số hay một biểu thức với tần suất quan sát được như trong tính toán giá trị trung bình ở trên. Ở đây tồn tại một cặp quy tắc tính toán chung có liên quan đến toán tử giá trị mong đợi, các giá trị này được suy diễn bởi cách tính toán trực tiếp:
Giá trị mong đợi tổng của một số các thông số ngẫu nhiên là tổng giá trị mong đợi của từng thông số ngẫu nhiên:
E[X1 + … + Xn] = E[X1] + … + E[Xn]
Giá trị mong đợi của tích của một hằng số và một thông số ngẫu nhiên là tích của hằng số và giá trị mong đợi của thông số ngẫu nhiên:
E[aX] = aE[X]
Tương tự, hiệp biến Var[X] của một thông số ngẫu nhiên được xác định bởi toán tử giá trị mong đợi:
Giới thiệu:
Trên nguyên tắc, mọi người chấp nhận rằng số lớp trong một giường trộn là yếu tố quyết định đối với độ đồng nhất thu được. Theo cái gọi là lý thuyết thống kê của giường trộn, sự giảm độ sai lệch tiêu chuẩn từ các nguyên liệu đầu vào đến các nguyên liệu đầu ra có quan hệ với căn bậc hai của số lớp nguyên liệu được rút đồng thời. Tuy nhiên, với các kho chứa có liên quan đến khái niệm trung bình động (điển hình là kho tròn vận hành theo phương thức Chevron liên tục), thời gian các loạt thay đổi thành phần của nguyên liệu đầu vào đóng vai trò phụ và đáng kể. Đây là phân tích trên lý thuyết bằng thống kê đại cương và có dính líu tới cỡ hạt liên quan đến khối lượng mẫu trong đánh giá các phép thử trộn.
Trong một kho chứa đồng nhất nguyên liệu thô, một đống được rải bởi số lớn lớp, sau đó chúng được rút ra theo cách nào đó sao cho tất cả các lớp đã rải đều có mặt trong vật liệu được rút ra. Để tính hiệu quả trộn trên lý thuyết có thể mong đợi từ những điều kiện như vậy, ta cần nhắc một chút về lý thuyết thống kê.
Bối cảnh thống kê.
Đặc tính của các thông số ngẫu nhiên là không bao giờ biết chính xác được giá trị của nó. Số phép đo có thể thực hiện và từ các phép đo này đánh giá sự phân bố hay tính toán định lượng các tính chất (như giá trị trung bình, hiệp biến, …). Để xác định cách định lương các tính chất này ra sao, hãy xem xét thông số ngẫu nhiên X và giả sử rằng một số phép đo cụ thể độ lớn của thông số này đã được thực hiện. Đã quan sát được các giá trị sau x1, x2, …, xn và chúng xuất hiện với tần suất f(x1), f(x2), … , f(xn), ở đây:
Giá trị mong đợi E[X] (tức là giá trị mong muốn nhất) của thông số ngẫu nhiên của chúng ta X được xác định là giá trị trung bình:
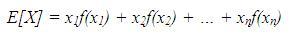
Các giá trị mong đợi của toán tử E[] sẽ luôn luôn liên quan đến trọng lượng, một thông số hay một biểu thức với tần suất quan sát được như trong tính toán giá trị trung bình ở trên. Ở đây tồn tại một cặp quy tắc tính toán chung có liên quan đến toán tử giá trị mong đợi, các giá trị này được suy diễn bởi cách tính toán trực tiếp:
Giá trị mong đợi tổng của một số các thông số ngẫu nhiên là tổng giá trị mong đợi của từng thông số ngẫu nhiên:
E[X1 + … + Xn] = E[X1] + … + E[Xn]
Giá trị mong đợi của tích của một hằng số và một thông số ngẫu nhiên là tích của hằng số và giá trị mong đợi của thông số ngẫu nhiên:
E[aX] = aE[X]
Tương tự, hiệp biến Var[X] của một thông số ngẫu nhiên được xác định bởi toán tử giá trị mong đợi:

